堆排序

堆排序是依赖堆的特性完成的排序。

堆分为小顶堆和大顶堆，堆是满二叉树结构且每个节点都是这个节点子树的最大或最小值，这样的结构为堆。根节点大的为大根堆，根节点为小的为小根堆。

堆排序，首先将数组映射成一个堆结构。可以映射成堆结构的原因是：数组的每个位置可以映射到堆的每个节点上。

排序原理：

我们现将数组的每个元素构造成大顶堆，然后逐个将堆顶与堆底交换，然后将堆底从堆中移除，重新维护大顶堆结构。周而复始可以将每个元素排好序。

如下图可以直观的感受数组和堆结构位置的映射关系

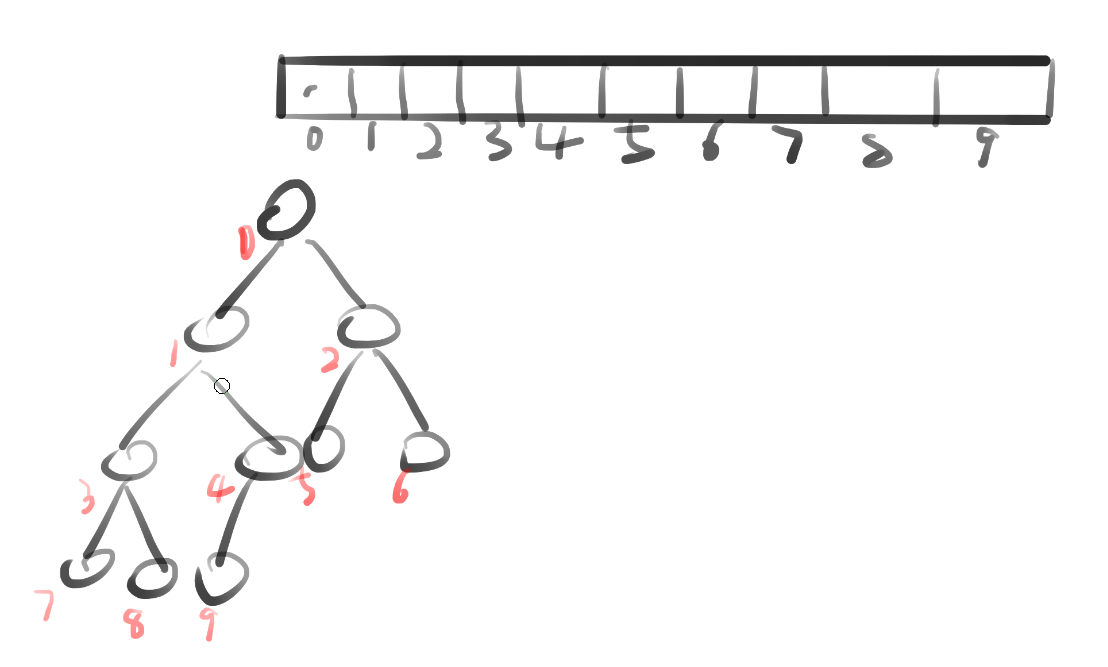
可以看到，重点的就是堆结构的维护。
插入：比较当前节点的父节点大小，比父节点大交换，直到不比父节点大或到达堆顶

更新：与两个子节点大的数比较，如果比节点小交换，直到比两个子节点都大或到达叶子节点

代码实现

package learn.note.algorithm.sort.three;

import java.util.Arrays;

public class HeapSort {
    public static void main(String[] args) {
        int[] list = new int[]{9,28,43,50,76,90,86,94,94,97};

        heapSort(list);
        // 对数器
        CompareMachineUtil.compare(HeapSort::heapSort, null);
        Arrays.stream(list).forEach(System.out::println);
    }

    private static void heapSort(int[] list) {
        if (list == null || list.length <= 1) {
            return;
        }
        int heapIndex = 0;
        // 构建大顶堆
        for (int i = 0; i < list.length; i++) {
            heapInsert(list, heapIndex++);
        }

        // 将最后一个与从大顶堆堆顶交换，断掉最后一个与堆的联系。重新维护大顶堆
        while (heapIndex > 0) {
            swap(list, --heapIndex, 0);
            heapify(list, 0, heapIndex);
        }
    }

    private static void heapify(int[] list, int index, int heapIndex) {
        int left = index * 2 + 1;
        while (left < heapIndex) {
            int largest;
            if (left + 1 >= heapIndex) {
                // 只有一个孩子
                largest = left;
            } else {
                // 俩孩子比较大小
                largest = list[index * 2 + 1] > list[index * 2 + 2] ? index * 2 + 1 : index * 2 + 2;
            }
            largest = list[largest] > list[index] ? largest : index;

            if (largest == index) {
                break;
            }
            swap(list, largest, index);
            index = largest;
            left = index * 2 + 1;
        }


    }

    private static void heapInsert(int[] list, int heapIndex) {
        // 这里要减一
        while (list[heapIndex] > list[(heapIndex - 1) / 2]) {
            swap(list, heapIndex, (heapIndex - 1) / 2);
            heapIndex = (heapIndex - 1) / 2;
        }
    }


    private static void swap(int[] list, int i, int j) {
        int temp = list[i];
        list[i] = list[j];
        list[j] = temp;
    }
}

视频讲解