排序 分类

计数排序

计数排序（Counting Sort）是一种非比较型的排序算法，适用于对整数或有限范围内的数据进行排序。它的核心思想是通过统计每个元素的出现次数，然后根据统计结果将元素放回正确的位置。计数排序的时间复杂度为 $O(n + k)$ ，其中 n 是待排序元素的数量，k 是数据的范围大小。

牧歌2025/8/18...大约 3 分钟

堆排序

堆排序是依赖堆的特性完成的排序。

堆分为小顶堆和大顶堆，堆是满二叉树结构且每个节点都是这个节点子树的最大或最小值，这样的结构为堆。根节点大的为大根堆，根节点为小的为小根堆。

堆排序，首先将数组映射成一个堆结构。可以映射成堆结构的原因是：数组的每个位置可以映射到堆的每个节点上。

排序原理：

我们现将数组的每个元素构造成大顶堆，然后逐个将堆顶与堆底交换，然后将堆底从堆中移除，重新维护大顶堆结构。周而复始可以将每个元素排好序。

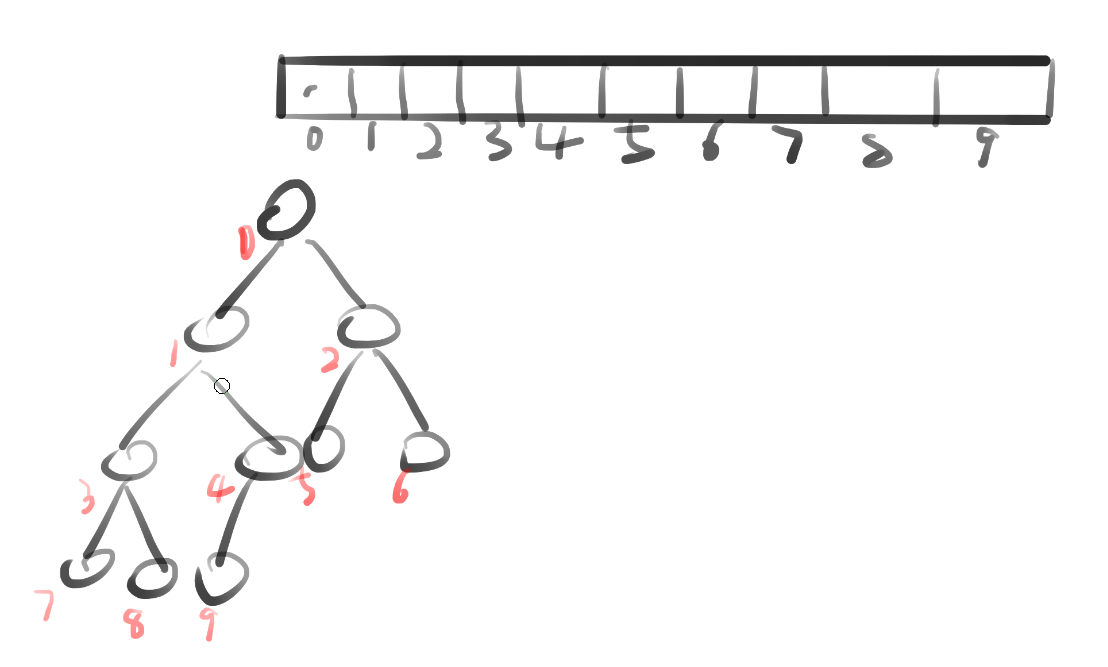
如下图可以直观的感受数组和堆结构位置的映射关系

image.png|950

牧歌2025/8/16...大约 2 分钟

归并排序以及衍生小和、逆序对问题

package learn.note.algorithm.sort.three;

import java.util.Arrays;

/**
 * @author Wang WenLei
 * @date 2025/7/30 17:29
 * @since 1.0
 */
public class MergeSort {
    public static void main(String[] args) {
        int [] data = {5,4,3,2,1};
        mergeSort(data);
        Arrays.stream(data).forEach(System.out::print);

        // 对数器
        CompareMachineUtil.compare(MergeSort::mergeSort, null);
    }

    public static void mergeSort(int [] data) {
        mergeSort(data,0,data.length-1);
    }

    public static void mergeSort(int [] data,int low,int high){
        if (data == null || high - low < 1) {
            return;
        }
        int middle = low + ((high - low) >> 1);
        mergeSort(data,low,middle);
        mergeSort(data,middle + 1, high);
        // 合并
        merge(data,low,middle,high);
    }

    private static void merge(int[] data, int low, int middle, int high) {
        int[] tempArr = new int[high - low + 1];
        int i = 0;
        int p1 = low;
        int p2 = middle + 1;

        // 这里都需要等于，左边是从0开始到分界点。右边是从分界点+1开始到数组结束
        // 边界都是闭区间，所以需要等于
        while (p1 <= middle && p2 <= high) {
            if (data[p1] < data[p2]) {
                tempArr[i++] = data[p1++];
            } else {
                tempArr[i++] = data[p2++];
            }
        }
        while (p1 <= middle) {
            tempArr[i++] = data[p1++];
        }
        while (p2 <= high) {
            tempArr[i++] = data[p2++];
        }

        for (i = 0 ; i < tempArr.length ; i++) {
            data[low + i] = tempArr[i];
        }
    }
}

牧歌2025/7/30...大约 3 分钟

插入排序

程序角度表述：
0位置本身有序，从1开始
从0-1，比较0、1位置的数大小，如果 0 比 1 位置数大交换
从0-2，逐个比较2&1、1&0位置的大小，直到前一个位置的数小停止
。。。
从0-n，逐个比较n&n-1、...、1&0位置大小，直到前一个位置的数小停止。

时间复杂度： $O(n^2)$

牧歌2025/7/24...小于 1 分钟

选择排序

按自然数从1开始数：
从 1到n 中选择一个一个最小的数，放到第 1 位置上
从 2到n 中选择一个一个最小的数，放到第 2 位置上
从 n-1到n 中选择一个一个最小的数，放到第 n-1 位置上
从 n到n中选一个最小的数，就是本身，放到 n 位置上

按程序数从0开始数：
从 0到n-1 中选择一个一个最小的数，放到第 0 位置上
从 1到n-1 中选择一个一个最小的数，放到第 1 位置上
从 n-2到n-1 中选择一个一个最小的数，放到第 n-2 位置上
从 n-1到n-1中选一个最小的数，就是本身，放到 n-1 位置上

牧歌2025/7/23...大约 1 分钟